题目：Self Crossing

You are given an array x of n positive numbers. You start at point (0,0) and moves x[0] metres to the north, then x[1] metres to the west,x[2] metres to the south, x[3] metres to the east and so on. In other words, after each move your direction changes counter-clockwise.

Write a one-pass algorithm with O(1) extra space to determine, if your path crosses itself, or not.

Example 1:

Given x = [2, 1, 1, 2],┌───┐│   │└───┼──>    │Return true (self crossing)

Example 2:

Given x = [1, 2, 3, 4],┌──────┐│      │││└────────────>Return false (not self crossing)

Example 3:

Given x = [1, 1, 1, 1],┌───┐│   │└───┼>Return true (self crossing)

给定一个数组，按照4个一个周期对应上、左、下、右四个方向的移动距离，判断给定数组是否会穿过自身移动的轨迹。

思路1：

分情况讨论，

 第一种情况如下：

┌───┐│   │└───┼>

它的条件很容易发现是A[i-1]<=A[i-3]&&A[i]>=A[i-2]

第二种情况如下：

 

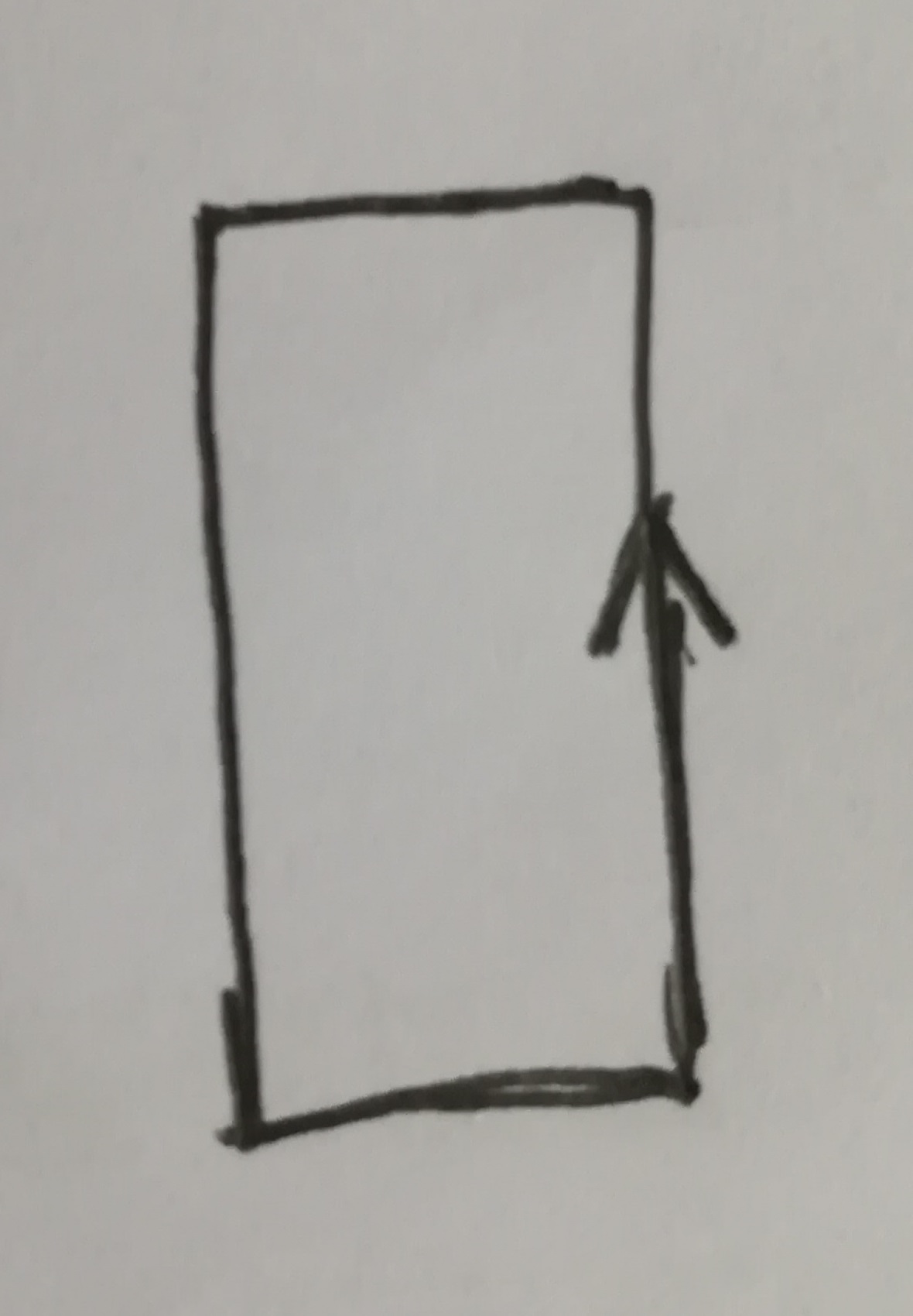
它的条件也很容易找到：i>4&&A[i-1]==A[i-3]&&A[i]+A[i-4]>=A[i-2]

第三种情况如下：

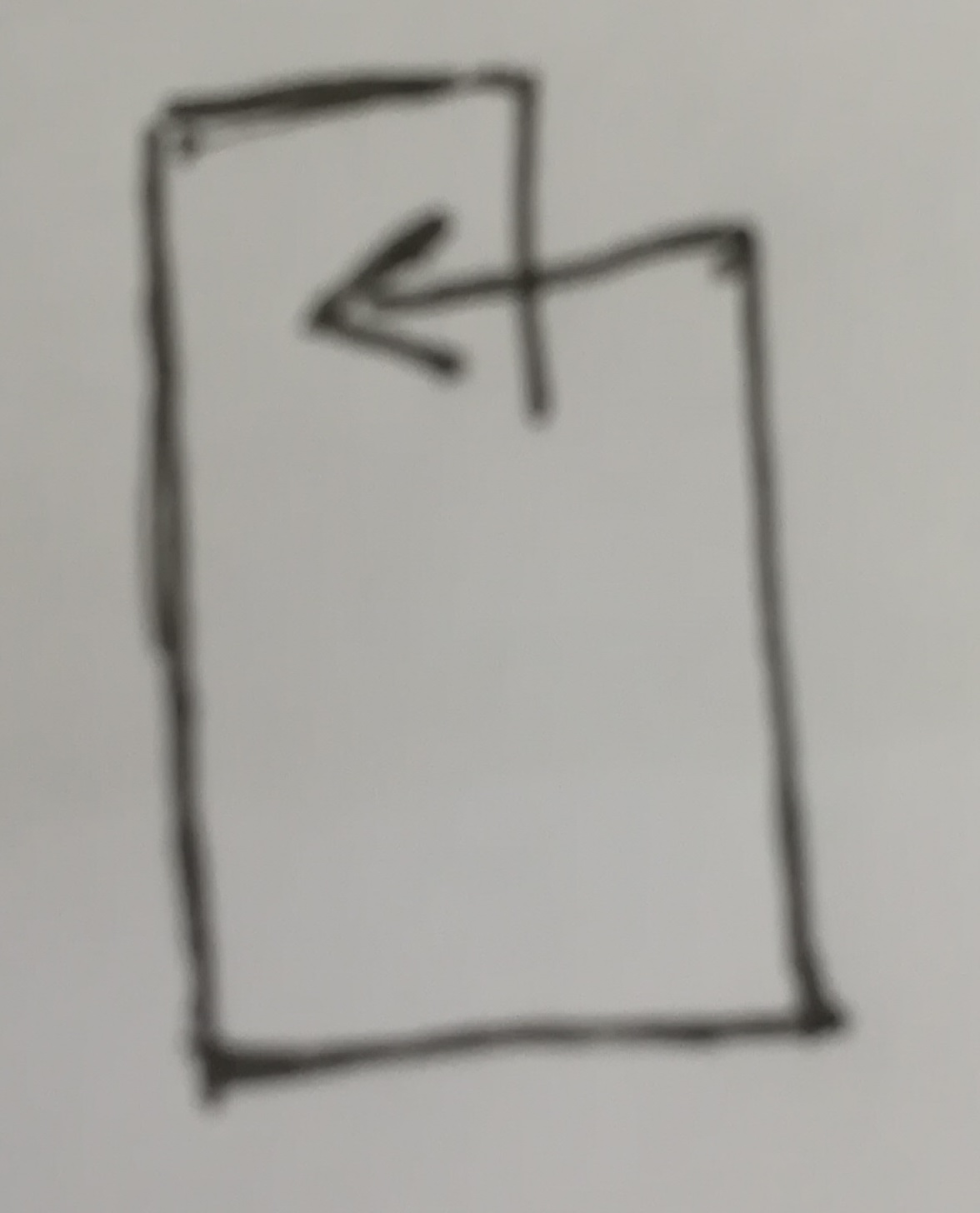
它的条件就要复杂一点：

i>5&&A[i]+A[i-4]>=A[i-2]&&A[i-1]+A[i-5]>=A[i-3]

同时注意还要满足：A[i-1]<=A[i-3]&&A[i-2]>=A[i-4]

于是就可以得到下面的判断程序：

bool isSelfCrossing(vector
     
      & x){    for (size_t i = 3; i < x.size(); ++i){        //i == 3时，穿过自身的情况；自己画图可以很容易推断出该情况下的条件        if (x[i - 1] <= x[i - 3] && x[i - 2] <= x[i])return true;        //i == 4时，穿过自身的情况；注意i-1==i-3相等时的情况，此时，需要比较i+i-4和i-2的大小        if (i > 3 && x[i - 1] == x[i - 3] && x[i] + x[i - 4] >= x[i - 2])return true;        //i == 5时，穿过自身的情况；在上面相等时的描述下，还需注意，可能会有最外层穿过其里面一层环的情况。        if (i > 4 && x[i - 1] + x[i - 5] >= x[i - 3] && x[i] + x[i - 4] >= x[i - 2] && x[i - 1] <= x[i - 3] && x[i - 2] >= x[i - 4])return true;    }    return false;}
     

思路2：

这个思路就很巧妙，不去考虑穿过自身的情况，而去考虑不会穿过自身的情况。如果想要这样一直不穿过自身只有两种趋势：

第一种趋势是螺旋增大；第二种趋势是螺旋减小。

于是就可以得到下面的程序：

bool isSelfCrossing2(vector
     
      & x){    x.insert(x.begin(), 4, 0);//插入4个0，统一判断    int len = x.size();    int i = 4;    //未穿过自身的形状大多是外螺旋加1个或0个内螺旋    //外螺旋，边逐渐增大    for (; i < len && x[i] > x[i - 2]; i++);    if (i == len) return false;    //判断外螺旋变为内螺旋时，是否会穿过自身    if (x[i] >= x[i - 2] - x[i - 4]){        x[i - 1] -= x[i - 3];    }    //内螺旋，边逐渐减小    for (i++; i < len && x[i] < x[i - 2]; i++);    return i != len;}